Who said ordinary folks don't have fun with math?

[Math Awesomeness, Facebook]

Don Knuth takes Wrong Turn on the Dragon

So Don Knuth is also an artist and errator [my term for someone who makes errors but it turns out that "errator" is Latin for "wanderer", which applies to Knuth and the curve he describes.]

A New Chuck Norris Fact

Time slows down the closer you get to the center of a black hole because that is where Chuck Norris Hangs out.

[ I made up this one, 2011-09-22]  

When I told it to my son, he said: "Time would just run away." 

To which I replied: "Nothing can escape Chuck Norris."

The Math and Logic of Yogi Berra

Math

• You better cut the pizza in four pieces because I'm not hungry enough to eat six.

• A nickel ain't worth a dime anymore.
  

• Baseball is ninety percent mental and the other half is physical.
  

• Another variation: Ninety percent of this game is half mental.
  

• Half the lies they tell about me aren't true.
  

• You have to give 100 percent in the first half of the game. If that isn't enough, in the second half, you have to give what is left.

Logic

• The future ain't what it used to be.
  

• I really didn't say everything I said.
  

• I usually take a two hour nap from one to four.
  

• Never answer an anonymous letter.

• In theory there is no difference between theory and practice. In practice there is.

• Nobody goes there anymore. It's too crowded.
  

• On why NY lost the 1960 series to Pittsburgh: We made too many wrong mistakes.
  

• It gets late early out here.
  

• If you don't know where you're going, you'll wind up somewhere else.

• If I didn't wake up I'd still be sleeping.
  

• Our similarities are different.
  [said by Dale Berra, Yogi's son, according to Retrogalaxy.com's Yogi-Berra.]
  

• I always thought that record would stand until it was broken.

• We have a good time together, even when we're not together [talking about his wife Carmen].
  

• Asked if first baseman Don Mattingly had exceeded expectations, Yogi said "I'd say he's done more than that!"

[Various online sources, including YogiBerra.com's Yogi-isms and Retrogalaxy.com's Yogi-Berra]

Have You Conside that ...? (Thinking differently)

Fact: Most people have more than the average number of legs.

[Source: Joke #25, "31 Jokes for Nerds", YouTube Video, posted by Vlogbrothers]

(This observation is correct for all parts of the body.)

One One One and One One

One One One was one racehorse,
One One was one too.
One One One won one race,
One One won one too.

More Is Not Always…

Q: What’s worse than getting a flat tire?

A: Getting two flat tires.

Q: What’s worse than finding a worm in your apple?

A: Finding half a worm in your apple

Math Is the Science of Patterns, Including This One

Patterns come in all sizes and shapes, delighting our senses. Here is one pattern that entertains the ear, the eye and the sense of rhythm.

When 15 > 25?

A customer walked into our auto-parts store looking for a flat washer. "That'll be 15 cents," I said.

"Fifteen cents for a washer? Are you crazy?" he yelled. "I'll drill a hole in a quarter and make my own."

Jack Reeves

[Source: Reader's Digest, August 2009, @Work (p. 67)]

Amelia's Dance = the Body as a Math Visual Aid

In her YouTube video, Amelia entertains us by turning her body with dance into a mathematical visual aid. She also demonstrate the endless ways one can present mathematical concepts.

Driving Math with the Math of Driving

Driving is a serious matter but this is funny.

Visiting family in Kentucky is a heart-stopping experience if only because my brother-in-law drives in the middle of the road, straddling the double yellow lines that separate traffic. My sister-in-law does little to ease my fears. Seeing the horror in my eyes, she once said, "Don't worry. Everyone around here drives in the middles of the road."

Lisa Walters, Ypsilanti, Michigan

[Source: Reader's Digest, June 2009, Life (p. 198)]

10,000 Left Shoes

Who would ever want to have 10,000 left shoes?

Well, here is a story that has stuck in my head for many years. I may be off on the specifics but I believe the just of it is true. And, if not, it could have happened or, in storytelling parlance, it’s plausible.

As I recall, in the mid 1960’s in Israel I read in the paper that a shipment of 10,000 left shoes had arrived in the port of Haifa from Italy. At the time, custom duty rates in Israel were extremely high, especially on such luxury imports. So the importer did not claim the shoes. Besides, what would he do with 10,000 left shoes? Stuck with this load, the custom office did what most custom agencies do with abandoned stuff, it auctioned it off. But no one had any use for 10,000 left shoes so no one made any bid. Well, eventually the original importer made a very low bid and the custom office was happy to get rid of the shoes that took space in its warehouse. So the importer got his 10,000 left shoes practically paying no duty.

A month or two later a shipment of 10,000 right shoes arrived in the port of Haifa and the same importer did not claim them because he did not want to pay the duty…

Surely, you have figured out by now the rest of the story.

Where is the math in this story?

It has to do with sets and how sets can be split, added up and rearranged. A pair of shoes is a set, a very useful set. It can be sold. 10,000 pairs is a set of 10,000 such useful sets. Splitting these pairs into 10,000 left shoes and 10,000 right shoes generates 2 sets containing 10,000 of useless shoes, which no one wants to buy. But then, whoever has both sets can recombine them to form the original 10,000 sets of sellable pairs of shoes.

Right on Time

A student returned home from a date at 3 AM. Her parents were very upset, "You're late! You said you'd be home by 11:45!"

"Actually," the girl replied, "I'm right on time. I said I'd be home by 1/4 of 12."

[Origin: unknown; several variations of this joke appear on various web; a version of this joke, submitted by Zhang Wenyi, was published in Reader's Digest, July 2009, "Laugh!:)", p. 27]

Mathematical Chuck Norris Facts

For the unfamiliar, there is a class of jokes about how awesome Chuck Norris is. Here I will post those with mathematical twist.

• Chuck Norris counted to infinity, twice.
[www.chucknorrisfacts.com, as of 2009-02-22]

• Chuck Norris knows the last digit of pi.
[www.chucknorrisfacts.com/page8.html, as of 2009-02-22]

• Chuck Norris can divide by zero.
[www.chucknorrisfacts.com/page2.html, as of 2009-02-22]

• If you have five dollars and Chuck Norris has five dollars, Chuck Norris has more money than you.
[www.chucknorrisfacts.com, as of 2009-02-22]

• The square-root of -1 is not imaginary. It's just hiding from Chuck Norris.
[Ben, 2009-02-22]

• The shortest distance between two points is Chuck Norris.
[org.]

• The square root of 2 is rational number for Chuck Norris.
[org.]

• Chuck Norris can square the circle, double the cube and trisect an angle using only his fingers for a compass and his arm for a straight edge.
[org.]

Subtraction Without Borrowing

clipped from www.youtube.com Subtraction Without Borrowing by MathVentures [Video Prototype 01]

This is my first video prototype. Lots of room for improvement,

clipped from www.youtube.com Clay Shirky: Institutions vs. collaboration

Testing Probability

Flummoxed by his true-false final exam, a student decides to toss a coin up in the air. Heads means true; tails, false. Thirty minutes later, he is done, well before the rest of the class. But then the student startsd flipping the coin again. And soon he's swearing and sweating over each question.

"What's wrong?" asks the concern teacher.

"I'm rechecking my answers," says the student.

[Comic Wendell Potter, Laugh!:), Reader Digest, March 2009, p. 81]

Uri's Comment: It is interesting to note that the student can change any answer that is not confirmed without affecting the probable grade of the test. Of course, for this to be true, the number of questions should be as large as possible. Considering that (a) it took the students 30 min. to finish the test and (b) it takes under 6 seconds to toss a coin and jot down the result, the test could have consisted of 150-300 questions (no need to spend time on reading each question). This test consists of a sufficient number of questions for probability to determine the overall grade.

Abbott and Costello, 13 x 7 = 28 (ver. 2, Selling Vacuum Cleaners)

Math Riddle No. 1

"To be or not to be," that is the answer.

What is the question?

Solution

Theo Jansen Invent Artificial Life and a New Wheel

Having the modest goal to create artificial life, Theo Jansen not only invented a new wheel, a better wheel, and employed math, geometry and science to new extremes but also successfully accomplished his goal.

Theo Jansen: The art of creating creatures

Visual Statistics - a Powerful Mathematical View of the World

Hans Rosling: Watch the end of poverty

With the right mathematical tools, starting with numerical data and using visual representation, Hans Rosling, a Swedish statistician, present an alternative view of the geopolitical world.

Alan Kay: A powerful idea about teaching ideas (TED, 2007)

Alan Kay's brilliant Math-learning tool.

Alan Kay: A powerful idea about teaching ideas

Auditory & Visual Patterns: The Raspyni Brothers Juggle at TED (Feb. 2008)

Starting at 11:30 (min:sec) of the video clip, listen to the sound of the juggling pins as they hit the jjgglers' palms - the rhythm is an auditory pattern. Freeze frame the video and see their trajectories. These are visual geometric patterns. The two types of patterns coincide.

clipped from www.youtube.com Raspyni Brothers: Welcome to Vaudeville 2.0

Brain Teasers, Word Puzzle No. 1

The words listed below have something in common. What is it? For an extra reward, i.e., more satisfaction, can you arrange them in the proper sequence according to this common trait of theirs? And for even more satisfaction, if you are up for the challenge, add the last word of the sequence.

A hint, one word in the list does not share the common attribute. However, in one important respect it does belong to the sequence and therefore serves as a hint to the solution.

The given words are:

Reflection, Cheers, Thousand, Alpha, Scotch, American, Steady, Father, Fourth, Winner, Inn

Solution

Is More Always Worse?

Is it always true that if you have a good thing, then having more of it is better and, conversely, if you got something bad having more of it is worse? Case in point, consider the following situation, which is usually told as a joke:

"What is worse than finding a worm in the apple you are eating?"
"I don't know... Two worms."
"No. Half a worm!"

Marching Band - Visual and Audio Pattern

UCLA Marching Band Strike Up the Band For UCLA

Drumline - An Audio Pattern People Enjoy

2006 UCLA Drumline

The Wave - Thousands of People Sharing Fun, Clip No. 2

Alabama A-Day Game 2007: Crowd Doing The Wave

Thousands of people enjoy doing and watching the wave. The sense of comradeship and sharing is most powerful. But the the beautiful pattern created by the synchronized crowd is magnificent.

The Wave - Thousands of People Sharing Fun, Clip No. 1

Thousands of people enjoy doing and watching the wave. The sense of comradeship and sharing is most powerful. But the the beautiful pattern created by the synchronized crowd is magnificent. You can hear the excitement in the voice of the woman.
[USC vs. Arizona State Football Game]

USC vs. Arizona State - Football Game Wave!

Shoelace Tying

I am always amazed at the ingenuity of the human mind. I've always been interested in and even fascinated by knots and tying. I've known several ways of tying shoelaces and did not give it much thought. I considered it so simple, once it was tied, the shoelace knot is one of the most basic knots. nothing to it.

Wrong!

Several years ago, when my son was in first grade I was awed by one of his classmates, a second grader, when I saw how she tied her shoelaces in a single, fluid motion. I asked her to repeat it and she did but her fingers always moved too fast for my eyes to catch the details of her action. The result, however, was the familiar knot. She told me that this is the only way she knew to tie her laces.

Then I came across this video and I learned how to tie my shoelaces in the same way.

It's not difficult and you can do it too and fascinate your friends.

The I Divide and You Decide Method for Splitting Ice-cream, Slicing Cake and Dividing All Sorts of Things Without Losing Your Friends

Editorial note. This posting was inspired by Math Doesn't Suck by Danica McKellar. I had written notes about this subject for this blog a while ago and I have taught it to students. As a matter of fact it is a popular "trick" parents use to squelch feuding kids. But the "Cake Cutting Problem" [as described in Wikipedia] is a very important mathematical subject [see also Math World's "Cake Cutting".] But when I read Math Doesn’t Suck and, in particular, the Chapter 7, "Is Your Sister Trying to Cheat You out of Your Fair Share? Comparing Fractions", I got the idea to tell it as a situation-story for kids. Danica writes for girls, especially of middle-school age. I write for everyone, especially kids, girls and boys, and adults too. So the situation I describe here is ageless and genderless.

One weekend you have your best friend for a sleepover. The two of you make a tent and crawl into your sleeping bags in your bedroom and as usual you stay up late. You go silent and pretend you’re asleep till your parents go to sleep. Then you turn on your flashlights and whisper stories and jokes. You get hungry and decide to raid the fridge. In the freezer you discover the partially-eaten ice-cream. So you decide to split it. Silently you get the ice-cream scoop and two bowls and start to divvy it up. But soon the two of you get into an argument. “Not fair,” your friend whispers in protest. “You got more.” You try better but now your share looks too small to you. But you don’t want to admit it. You return all the ice cream from the bowls to the carton, give the ice-cream scoop to your friend and say, “You do it.”

Your friend tries and now you feel you don’t get your fair share.

The argument threatens to wake your sleeping parents. Worse, the ice cream is melting and both of you are craving it. What to do?

You have an idea. Since when one of you does it all the other person feels cheated, why not split the job? So you tell your friend, “I got it! I know what to do. I’ll divide the ice cream into the two bowls the best I can and then you will select which bowl is yours. This way neither of us has a reason to complain.” Your friend thinks about it for a moment. So you add, “It’s okay if we switch jobs. You can split the ice cream as best as you can and I’ll select my bowl.” Right away your friend says, “Okay.” And after a second adds, “that makes no difference.” Your friend got it. The ice cream is delicious and you and your friend sleep in late.

A few months later a friend has a birthday party. After the party the friend invites you and your best friend for a sleepover. In the middle of the night the three of you get a strong craving for the leftover birthday cake. You sneak to the kitchen and get the cake. Your friend, whose birthday cake it is, tries to slice the cake evenly between the three of you. But each time he cuts it one of you feels cheated. After a while your friend gives up. You recall how you split the ice cream so you say, “I know how to divide anything between two people so no one can complain but I don’t know what to do when there are three of us.”

Your best friend says, “Hey, I know. One of us will slice a 1/3 of the cake. Then each of the other two get a turn to say if the cake is fairly divided into a 1/3 and 2/3 piece. If not, the person gets to adjust the slices and we start over. Once we have an agreement, one of the two who did not make the final cut gets the slice that is the 1/3. Then we have to divide what is left among 2 of us and this we know how to do.

It works and the three of you have a wonderful slumber party.

The following winter a group of friendly families go on a camping trip. One day you want a change from snowboarding and skiing. You decide to have a snowball fight. There is plenty of snow especially where the snowplow left a huge clean mound. But to be fair each fighter should have the same pile. People start to argue. But this time you know what to do right away.

You arrange your twelve friends in a circle, ordering them alphabetically by name, in front of the large snow mound. “Alice, you will take as much snow as you think it is fair for one person from this mound. When you are done, Carol, you get to decide if Alice’s pile is just right, too small or too large. If it is too small add to it and if it is too large take away from it. All snow is taken from or returned to this mound. Once you are done it’s your turn David to do as Carol did. We’ll go around all of us until no one makes any more changes to the pile that Alice started. Once that happens, the person after the last person to adjust the pile size gets this pile. For example, if Jeff is the last person to make any changes to the pile then Michelle gets it. Then we repeat the whole process again without Michelle.”

“It’ll take for ever,” Diane says.

“But it’s fair,” your best friend comes to your defense.

“If we want to play, we’ll do it fast,” you say.

So it’s agreed to give it a try and Alice starts. Soon no one can hold their hands idle any longer. There is simply too much snow around and the balls start flying. Who said everyone should get an equal pile when there is endless snow.

Congratulations. You and your friends discovered important principles of mathematical thinking: induction and recursion. Say you have a collection of things that you can order. In this collection some property is true for the first item. (We call this Rule A.) Also you know that any time this property is true for an item in the group, it is also true for the next item. (We call this Rule B.) This is called induction. Because, due to Rule A the first item has the property and therefore, because of Rule B, the second item has it too. But then by repeating Rule B so does item no. 3 and so on and so on… every item till the last item gets this property.

Recursion is when you repeat the same action again and again on a collection of things that grows smaller with each iteration till you must stop because you run out of those things.

You and your two friends recursively divided the birthday cake. It took only two steps but when the recursion ended all of you had no reason to feel cheated. And the reason it was so was induction. Then, for your snowball fight, you generalized your method and came up with your own procedure, or algorithm in geek-speak.

In Chapter 7 of her Math Doesn't Suck, Danica McKellar shows us how to avoid problems when things can be counted or measured precisely. Now you discovered that mathematical thinking is also helpful when things cannot be counted or measured. For if you could do that, you could have measured how much ice cream or cake each of you got and make the division by measuring. But that would have been too messy. Besides being fair and satisfied means different things to different people. Math came to the rescue with a simple, common sense method — I Divide and You decide!

Awesome.

Doube Negation, a Joke

The language teacher: "In most languages a double negative means the positive but in no language a double positive means the negative."

A student at the back of the classroom sneers: "Yeah, yeah!"

(According to John Allen Paulos this joke is based on a "true story" that took place during "a talk on linguistic" given by a "well-known philosopher", which he did not name. The person who responded with the double-positive was "another well-known philosopher." [Mathematics and Humor, p. 43.])

100-Meter Sprint/Dash -- a Source for Interesting Calculations

Asafa Powell Bonita Jamaica Fastest
Originally uploaded by Bonita Jamaica

On Sept. 9, 2007, Asafa Powell broke his own 100-meter sprint/dash world record, his new record is now 9.74 sec. This race and his record can be a source for interesting calculations:

1. How many steps it takes the runners to cover 100 m?

2. What is the average step size?

3. What is their speed in terms of mph?

4. How much time during the race they spend in the air (as oppose to touching the ground)?

This can be evaluated/estimated by viewing the video frame by frame.

I believe it is more than half the time.

Look at it another way, with respect to distance, not time:
Most of the 100-meter distance he covers while he is airborne. If so, in a sense, with respect to distance, he is flying. But this is a misrepresentation because he must touch the ground every step in order to propel his airborne self for the next segment of his “flight.”

5. Assuming that Asafa Powell's weight is still 88 kg (per Wikipedia's older article), then:

5.1. What is his acceleration?

5.2. How much force he spent?

5.3. How much energy?

Friendly Gifts/Favors and Mathematical Reasoning

It is common among friends and relatives of professionals to expect a favorable treatment, that is, a discount or a freebie, when they need the service or product of their professional friend. And it is almost just as common practice for the professional to oblige with such an expectation. For example, if you have a friend who is a plumber, I dare presume that, when your toilet is plugged and you urgently need a plumber, you might call your plumber friend, ask his assistance and expect him to give you a discount or perhaps even a freebie. You may then reciprocate buying him a dinner or a bottle of wine but the value of this thank-you gift is much lower than the value of the service.

Or, say, your friend is an author who just published a new book. You probably expect her to give you a free copy of the book, perhaps even an autographed one with a personal dedication.


My question is this:

In mutual relationship, why it is the pro who has to favor you? Why don’t you favor the pro?

Consider the example of your author friend. Why should she give you a free copy of her book? Why shouldn’t you buy her book and pay double its price?

OK, I know, the bookseller can’t take a payment larger than what they sell it for but you get the idea. Beside, we can figure out a workaround this formal limitation. For if you truly like your friend and want to (a) encourage her writing and/or (b) encourage her publisher to publish more of her books and/or publish more books of this kind, then you can send the extra payment with an explanation to either the publisher or your friend the author. Or at least, buy the hardbound book at a full-price retailer, not a paperback at discounter, and then, when the paperback comes out, buy it too.


Where is the math here?

Think of positive and negative numbers and especially think of the duality between the positives and negatives. In this case, why the positive should be a discount for you and the financial negative to your friend and not the other way around?

This is a clear example how positive and negative numbers are often set by the relevant context. For example, if I owe you money, then, as far as I am concerned, my debt to you has a negative value while, from your perspective the debt has a positive value. Similarly, for pilots going up is a positive experience and ascending is indicated by positive numbers and descending by negative numbers. On the other hand, for a scuba diver going into the ocean depth is a most positive experience, so for her descending is measured by positive numbers, which also indicate the increase in pressure, while ascending is measured by negative numbers.

When I talk to students, teachers and others about negative and positive numbers, I like to say:

There is nothing negative about the negative numbers.

Math Humor

I will start my collection of math humor with Abbott and Costello. For Abbott and Costello loved to perform funny mathematical routines. Some they performed in different settings. I once heard that they had a mathematician among their writers. Many of their mathematical skits are quite famous. I think that their most famous routine, “Who’s On First'” is funny because of its mathematical point of view (I will explain it in that post.)

Can you figure out why these skits are so funny? What is wrong with the math and how to fix it?

Abbott and Costello, 13 x 7 = 28 (ver. 1, Navy Cook)

Abbott and Costello, Two Tens for a Five

Abbott and Costello, The Loan

Abbott and Costello, Who's on First?

The mathematical connection of this famous routine is not obvious. But some important math concepts are at the root of this funny skit.

After you stop laughing and, if you are like me, wipe the tears so you can see straight, you may take a minute to think about why this is so funny. Clearly it is the use of ordinary words as proper names. But "who" and "what" are not just ordinary words. These are pronouns.

Considering the history of human languages, nouns, proper names and pronouns predate numbers, constants and variables by thousands of years. More importantly natural languages, like English and Chinese are much older than formal languages like the semantic aspect of mathematics. This is a very important point to keep in mind. For math, as a language, abhors ambiguities. Math cannot tolerate confusing numbers and variables. In mathematical terms proper nouns are numbers or constants and pronouns are are variables and in "Who's On First?" Abbott and Costello do just that -- they confuse numbers or constants with variables.

I include "Who's On First?" in my math-humor collection because what makes it funny is the absurd exchange. And these absurds are rooted in ambiguities that we may tolerate in most normal communications. For a few moments we are made to see, if not to understand, the mathematical viewpoint of such ambiguities. This is an excellent illustration of the connection of strict mathematical concepts to ordinary language. If we remember this fact, we can often make those formal mathematical ideas much easier to understand.

Subtraction Without Borrowing

I have written a procedure for dynamic subtraction, in which borrowing is replaced by dynamic addition and the subtraction that has to be done is much simpler: it is done within each place-value column, in any order; that is, subtracting the single-digit numbers in each column is completely independent of anything you do in any of the other columns. You can read more about it iin the following sites:

• MathVetures

1. Simplified Procedure
2. Original (light) Procedure
3. PDF download of this original version
4. Detailed Explanation (download a PDF file)

• Wikipedia

1. Subtraction Without Borrowing (my article)

Strange Numbers, Mixing Decimal Fractions with Ordinary Fractions

Although such number mix-ups are not common, I have seen them several times on gas stations. Finally I took some photos.

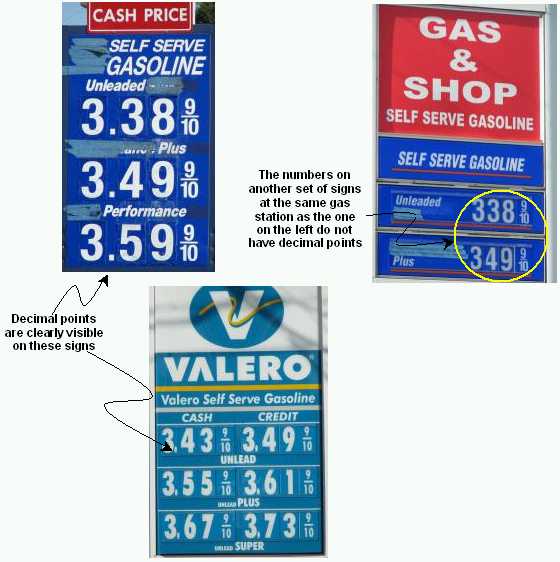
A few observations:

• I suspect that, if a student wrote an answer to a math problem in this form, the teacher will not accept it as valid.
  
• My son pointed out that these numbers are like having a second decimal point, such as 3.38.9, which is wrong.
• The values that these numbers represent are obviously clear; adding the decimal point, if noticed at all, causes no confusion: The ordinary fraction stands for 9/10 of a cent, not of a dollar.
• This can be viewed to be an example of mixed bases in the place-value columns, which is very acceptable and common practice but requires special notation. For example, the time 7:49:25.83 is correct and unambiguous. The different place values are separated by colons and a decimal point. The leftmost place value is either 12- or 24-base and may consist of a single digit or two; the next two place values are based 60 and the rightmost one is a decimal fraction of the preceding one (seconds), separated from it by a decimal point and, in this example, contains two decimal place values.
• The prices on the pumps at these gas stations are completely decimal, such as $3.389 and $3.499.

Does the inclusion of the decimal point add any more information? Does it serve any purpose? What did the people who placed the decimal points with the fractions tried to accomplish? Or is it the result of lack of understanding of how to express numerical values? (I did not ask any station attendant about their signs.)I am not questioning the presence of the 9/10 fractions because having them is a well-established practice in retail-gasoline pricing.

Question. Has anyone seen similar mixing of decimal fractions with ordinary fraction anywhere other than on gas-stations' price signs?

Math and Precision

Math is perfectly precise. It has to be. Math cannot depend on our ability to draw a straight line, calculate some result or on whether or not we can perform any other mathematical task. Mathematicians have recognized that, no matter how hard anyone tries, it is impossible to achieve, let alone maintain, the precision level math requires. So the mathematical system, which generations of mathematicians developed, accepts our imperfect capabilities and overcomes the drawbacks by maintaining a simple principle. We must be as precise as we can under the given circumstances and do our best to avoid ambiguities. Once we do that, our imprecise mathematical communications can represent perfectly precise mathematical thoughts.

What Is Math?

Math is the study of patterns and relationships.

Math explores the world, real and imaginary, by searching for, discovering and studying patterns and relationships. To do so, math employs logic, the art of reasoning. In turns, science, the study of figuring things out, which in turns employs math.